Econometrics I

TA Christian Alemán

Session 3: Friday 4, February 2022

Activity 1: Random Sampling

Simulate a Population

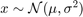
$x\sim\mathcal{N}(\mu,\sigma^{2})$

% Housekeeping
clear all
close all
clc
%
% Begin Script
rng(1234)                 % Set seed for reproductivity
%
% Simulate the Universe
% Plot options
par.num_bins  = 50;
opt.norm_type = {'count','pdf'};    % Normalization type
opt.sel_norm  = 2;                  % 1: count 2: pdf


par.N  = 1000000;         % Our Universe
par.NS = 50;             % Size of our sample
par.MS = 1000;           % Number of samples
par.sigma = [0.1,0.5];
par.mu    = 4;
vars.x_vec = NaN(par.N,2);
vars.x_sample = NaN(par.NS,par.MS,2);
vars.x_mean   = NaN(par.MS,2);
vars.y_sample = NaN(par.NS,par.MS,2);
vars.y_mean   = NaN(1,par.MS,2);
for i = 1:2

    vars.x_vec(:,i) =  par.mu + par.sigma(i).*randn(par.N,1);

With Loop: Generate NS number of samples from the universe.

    for j = 1:par.MS
        vars.x_sample(:,j,i) = randsample(vars.x_vec(:,i),par.NS);
        vars.x_mean(j,i) = mean(vars.x_sample(:,j,i));
    end

Without a loop Purely for Montecarlo Purposes:

    vars.y_sample(:,:,i) =  par.mu + par.sigma(i).*randn(par.NS,par.MS);
    vars.y_mean(1,:,i) = mean(vars.y_sample(:,:,i),1);

end

Plot the Distribution of Means and the true mean

figure(1)
subplot(2,1,1)
histogram(vars.x_mean(:,1),par.num_bins,'Normalization',opt.norm_type{opt.sel_norm});
xline(par.mu,'g-','linewidth',2)
xline(mean(vars.x_mean(:,1)),'r-','linewidth',2)
title(['$\sigma^{2} = $',num2str(par.sigma(1)^2)],'interpreter','latex','fontsize',17)
xlim([3.7,4.3])
legend({'Dist of the Mean','True','Estimated'})
ylabel(opt.norm_type{opt.sel_norm})
subplot(2,1,2)
histogram(vars.x_mean(:,2),par.num_bins,'Normalization',opt.norm_type{opt.sel_norm});
xline(par.mu,'g-','linewidth',2)
xline(mean(vars.x_mean(:,2)),'r-','linewidth',2)
title(['$\sigma^{2} = $',num2str(par.sigma(2)^2)],'interpreter','latex','fontsize',17)
xlim([3.7,4.3])
legend({'Dist of the Mean','True','Estimated'})
ylabel(opt.norm_type{opt.sel_norm})

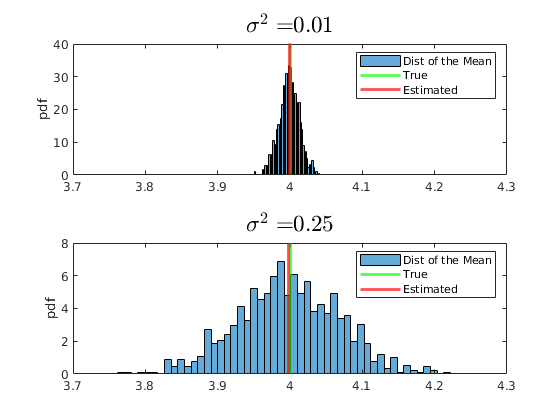
Do the same for the generalized pareto:

rng(567)                 % Set seed for reproductivity

par.sigma     = 0.1;  % Scale
par.k         = 0.8;  % Index, shape
par.theta     = 0;  % Threshold, location
vars.x_vec     = gprnd(par.k,par.sigma,par.theta,par.N,1);
par.MS        = 2000;
par.NS        = 200;             % Size of our sample
par.mu_A        = par.theta+(2^(par.k)-1).*par.sigma./par.k;
par.mu_B        = par.theta+par.sigma./(1-par.k);
% Initialize Matrix Holders
vars.x_sample = NaN(par.NS,par.MS);
vars.x_mean   = NaN(1,par.MS);
vars.x_median   = NaN(1,par.MS);
% Plot the histogram of the distribution of the Universe
I = vars.x_vec>4;
figure(2)
hold on
histogram(vars.x_vec(not(I)),par.num_bins,'Normalization',opt.norm_type{opt.sel_norm});
legend('Distribution of the Universe')
ylabel(opt.norm_type{opt.sel_norm})


for j = 1:par.MS
    vars.x_sample(:,j) = randsample(vars.x_vec,par.NS);
    vars.x_median(j) = median(vars.x_sample(:,j));
    vars.x_mean(j) = mean(vars.x_sample(:,j));
end

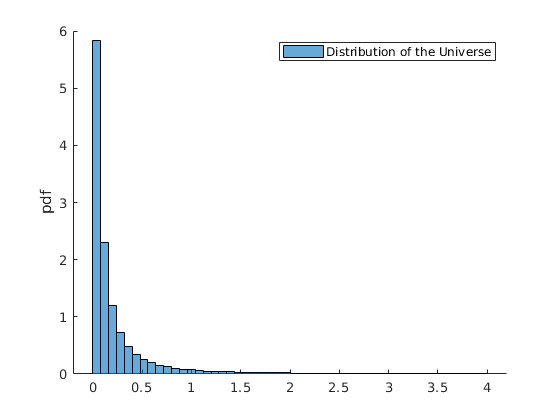
Plot the Distribution of Medians

figure(3)
%histogram(vars.x_mean,par.num_bins,'Normalization',opt.norm_type{opt.sel_norm});
%xline(mean(vars.x_mean),'r-','linewidth',2)
%xline(par.mu_B,'g-','linewidth',2)
histogram(vars.x_median,par.num_bins,'Normalization',opt.norm_type{opt.sel_norm});
xline(par.mu_A,'g-','linewidth',2)
xline(mean(vars.x_median),'r-','linewidth',2)
legend({'Dist of the Median','True','Estimated'})
ylabel(opt.norm_type{opt.sel_norm})

Activity 2: Backing out Residuals

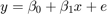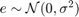
$y = \beta_{0} + \beta_{1} x + e$ Where $\,\,\,e\sim \mathcal{N}(0,\sigma^{2})$

%
rng(4567)
par.n = 500;
% Simulate x
par.mean_x1 = 4;
par.variance_x = 2;
par.variance_e = [0.1,0.3,0.8];
x = par.mean_x1 +sqrt(par.variance_x).*randn(par.n,1);
% Model coefficients:
par.beta0 = 2;
par.beta1 = 0.5;
% Simulate error
err = NaN(par.n,3);
y   = NaN(par.n,3);
for i = 1:3
    err(:,i) = 0 + sqrt(par.variance_e(i)).*randn(par.n,1);
    % Simulate Data Generating Process:
    y(:,i) = par.beta0 + par.beta1.*x +err(:,i);
    % Estimate the OLS and back out the Residuals
    if i ==1
        vars_1 = ols_esti(y(:,i),[ones(par.n,1) x]);
    elseif i ==2
        vars_2 = ols_esti(y(:,i),[ones(par.n,1) x]);
    else
        vars_3 = ols_esti(y(:,i),[ones(par.n,1) x]);
    end
end

figure(4)
hold on
grid on
plot(x,y(:,1),'kx')
plot(x,vars_1.y_hat,'b-','linewidth',1.1)
ylim([0,8])
xlabel('$x$','fontsize',17,'interpreter','latex')
ylabel('$y$','fontsize',17,'interpreter','latex')
title(['$\sigma^{2} = $ ',num2str(par.variance_e(1))],'interpreter','latex','fontsize',17)
figure(5)
hold on
grid on
plot(x,y(:,2),'kx')
plot(x,vars_2.y_hat,'b-','linewidth',1.1)
ylim([0,8])
xlabel('$x$','fontsize',17,'interpreter','latex')
ylabel('$y$','fontsize',17,'interpreter','latex')
title(['$\sigma^{2} = $',num2str(par.variance_e(2))],'interpreter','latex','fontsize',17)
figure(6)
hold on
grid on
plot(x,y(:,3),'kx')
plot(x,vars_3.y_hat,'b-','linewidth',1.1)
ylim([0,8])
xlabel('$x$','fontsize',17,'interpreter','latex')
ylabel('$y$','fontsize',17,'interpreter','latex')
title(['$\sigma^{2} = $',num2str(par.variance_e(3))],'interpreter','latex','fontsize',17)

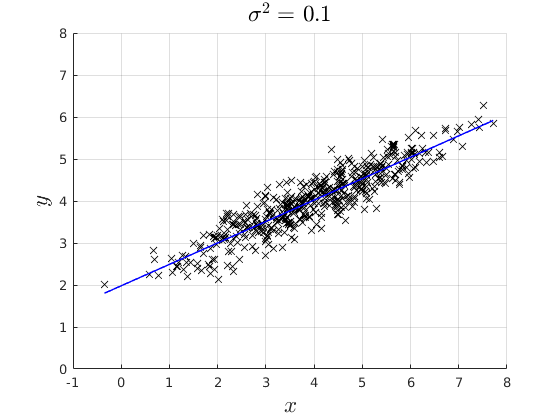
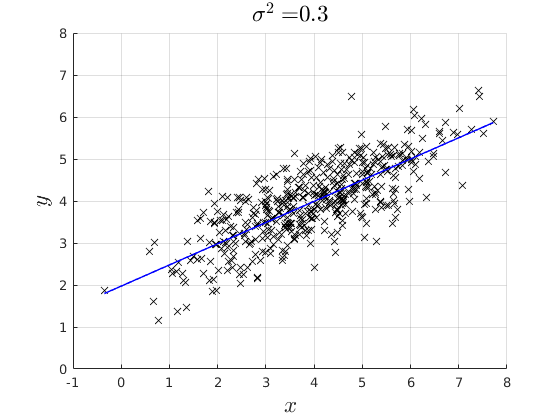
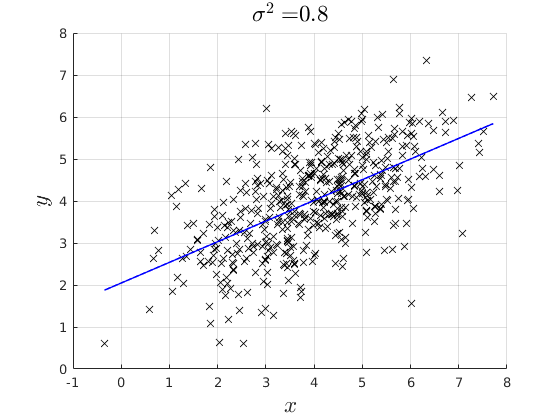
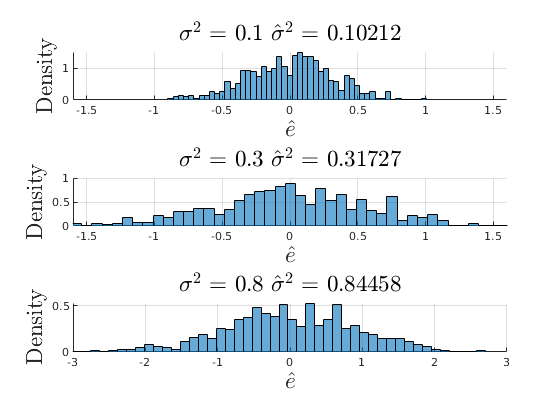
Plot the distrobution of the residuals
figure(7)
subplot(3,1,1)
hold on
grid on
histogram(vars_1.e_hat,par.num_bins,'Normalization',opt.norm_type{opt.sel_norm});
ylabel('Density','fontsize',17,'interpreter','latex')
xlabel('$\hat{e}$','fontsize',17,'interpreter','latex')
title(['$\sigma^{2}$ = ',num2str(par.variance_e(1)),'  $\hat{\sigma}^{2}$ = ',num2str(var(vars_1.e_hat))],'interpreter','latex','fontsize',17)
xlim([-1.6,1.6])
subplot(3,1,2)
hold on
grid on
histogram(vars_2.e_hat,par.num_bins,'Normalization',opt.norm_type{opt.sel_norm});
ylabel('Density','fontsize',17,'interpreter','latex')
xlabel('$\hat{e}$','fontsize',17,'interpreter','latex')
title(['$\sigma^{2}$ = ',num2str(par.variance_e(2)),'  $\hat{\sigma}^{2}$ = ',num2str(var(vars_2.e_hat))],'interpreter','latex','fontsize',17)
xlim([-1.6,1.6])
subplot(3,1,3)
hold on
grid on
histogram(vars_3.e_hat,par.num_bins,'Normalization',opt.norm_type{opt.sel_norm});
ylabel('Density','fontsize',17,'interpreter','latex')
xlabel('$\hat{e}$','fontsize',17,'interpreter','latex')
title(['$\sigma^{2}$ = ',num2str(par.variance_e(3)),'  $\hat{\sigma}^{2}$ = ',num2str(var(vars_3.e_hat))],'interpreter','latex','fontsize',17)
xlim([-3,3])

Activity 3: Understanding Collinearity

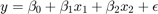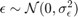
$y = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + \epsilon$ Where $\,\,\,\epsilon\sim \mathcal{N}(0,\sigma^{2}_{\epsilon})$

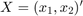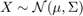and $X = (x_{1}, x_{2})'$ where $X \sim \mathcal{N}(\mu,\Sigma)$ with $\Sigma = \left[\begin{array}{cc}\sigma^{2}_{x_{1}} & \rho\sigma_{x_{1}}\sigma_{x_{2}} \\ \rho\sigma_{x_{1}}\sigma_{x_{2}} & \sigma_{x_{2}}^{2} \end{array}\right]$

Some Parameters we can play with:

  1. Number of Samples
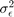
  2. Variance of the error $\sigma^{2}_{\epsilon}$
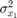
  3. Variance ofx $\sigma^{2}_{x_{1}}$
  4. Correlation 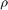$\rho$ between 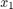$x_{1}$ and $x_{2}$
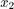
par.names = {'$\sigma^{2}_{\epsilon}$ ','$\sigma^{2}_{x_{1}}$ ','$\rho$ '};
% Data Generating process values:
grids.sigma_e  = [0.01,0.3,0.6,1,2.6,3];
grids.sigma_x1 = [0.01,0.1,0.8,1.6,2,2.5];
grids.rho      = [0,0.6,0.9,0.95,0.99,1];

% Default Values:


par.n  = 100;       % Sample size
par.ns = 1000;      % Number of Montecarlo Samples
% Simulate x
par.mean_x1 = 20;
par.mean_x2 = 27;
par.variance_x2 = 1.4;
% Model coefficients:
par.beta0 = 2;
par.beta1 = 0.3;
par.beta2 = 1.5;
% Simulate error
err = NaN(par.n,par.ns);
y   = NaN(par.n,par.ns);
X   = NaN(par.n,2,par.ns);
SE_beta_hat = NaN(par.ns,1);
beta1_hat   = NaN(par.ns,1);
mu_beta     = NaN(6,3);
mu_SEbeta   = NaN(6,3);
% Simulate Data Generating Process:
par. variance_e  = grids.sigma_e(2);
par. variance_x1 = grids.sigma_x1(3);
par. rho         = grids.rho(1);


for i = 1:3
    it = 0;
    for ii = 1:6
        % Defaults:

        if i ==1
            par.varianve_e = grids.sigma_e(ii);
            par.name_val = par.varianve_e;
        elseif i ==2
            par.variance_x1 = grids.sigma_x1(ii);
            par.name_val = par.variance_x1;
        elseif i ==3
            par.rho = grids.rho(ii);
            par.name_val = par.rho;
        end
        % Simulate the Correlated Variables

        par.big_sigma = [par.variance_x1,sqrt(par.variance_x1)*sqrt(par.variance_x2)*par.rho;sqrt(par.variance_x1)*sqrt(par.variance_x2)*par.rho,par.variance_x2];
        for oo = 1:par.ns
            % Generate the data
            rng((i*100000)+(ii*10000)+oo)
            err(:,oo) = 0 + sqrt(par.variance_e).*randn(par.n,1);
            X(:,:,oo) = mvnrnd([par.mean_x1,par.mean_x2],par.big_sigma,par.n);
            y(:,oo) = par.beta0 + par.beta1.*X(:,1,oo)+par.beta2.*X(:,2,oo) +err(:,oo);
            % Estimate OLS
            try
                vars = ols_esti(y(:,oo),[ones(par.n,1) X(:,:,oo)]);
                SE_beta_hat(oo,1) = vars.SEbeta_hat(2);
                beta1_hat(oo,1)   = vars.beta_hat(2);
            catch
                if oo ==1
                disp('Perfect Colinearity, check your variables!')
                end
                SE_beta_hat = NaN(par.ns,1);
                beta1_hat   = NaN(par.ns,1);
            end
            % Extract Values

        end

        mu_beta(ii,i)   =  mean(beta1_hat);
        mu_SEbeta(ii,i) =  mean(SE_beta_hat);
        % Compute and save the mean of the OLS estimator
        % Plot the Histograms
        if ii == 1|| ii == 3|| ii ==5
        it = it+1;
        figure(10+i)
        subplot(3,1,it)
        hold on
        histogram(beta1_hat,par.num_bins,'Normalization',opt.norm_type{opt.sel_norm});
        xline(par.beta1,'g-','linewidth',2)
        xline(mean(mu_beta(ii,i)),'r-','linewidth',2)
        ylabel('Density','fontsize',13,'interpreter','latex')
        xlabel('$\hat{\beta}$','fontsize',13,'interpreter','latex')
        title([par.names{i},' = ',num2str(par.name_val)],'interpreter','latex','fontsize',15)

        end
        par. variance_e  = grids.sigma_e(2);
        par. variance_x1 = grids.sigma_x1(3);
        par. rho         = grids.rho(1);
    end

end

Perfect Colinearity, check your variables!

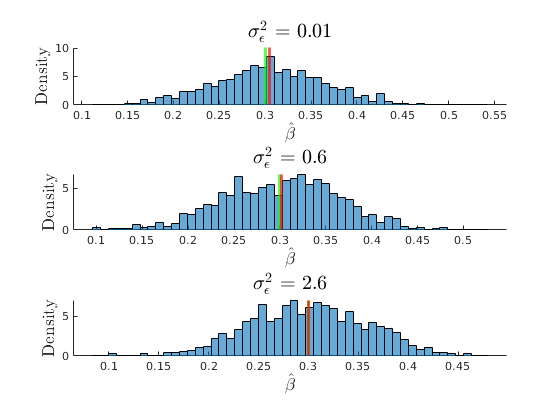
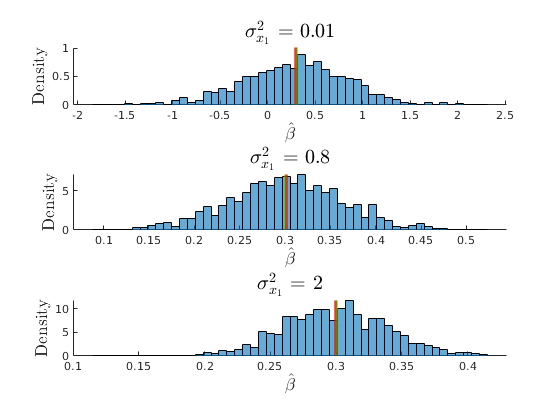
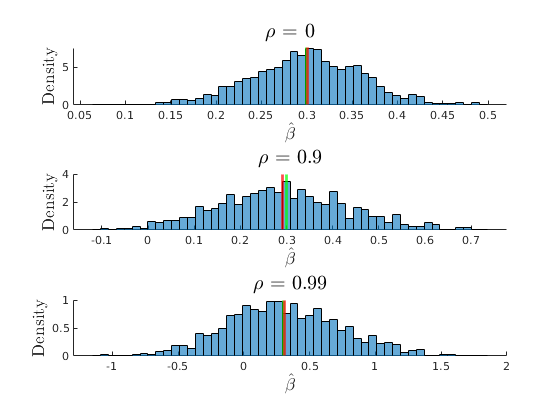
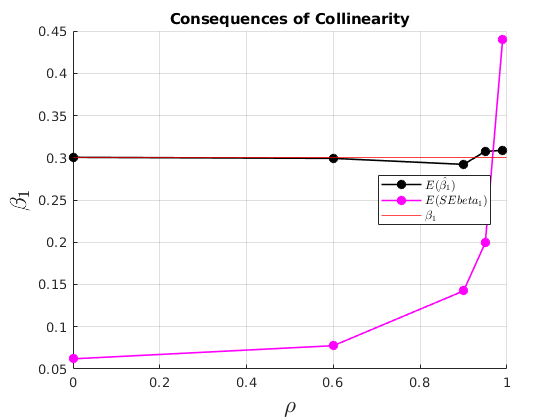
The consequences of collinearity

figure(33)
hold on
grid on
plot(grids.rho,mu_beta(:,3),'ko-','MarkerFaceColor','k','linewidth',1.2)
plot(grids.rho,mu_SEbeta(:,3),'mo-','MarkerFaceColor','m','linewidth',1.2)
yline(par.beta1,'r')
ylabel('$\beta_{1}$','interpreter','latex','fontsize',17)
xlabel('$\rho$','interpreter','latex','fontsize',17)
legend({'$E(\hat{\beta_{1}})$','$E(SEbeta_{1})$','$\beta_{1}$'},'interpreter','latex','location','best')
title('Consequences of Collinearity')

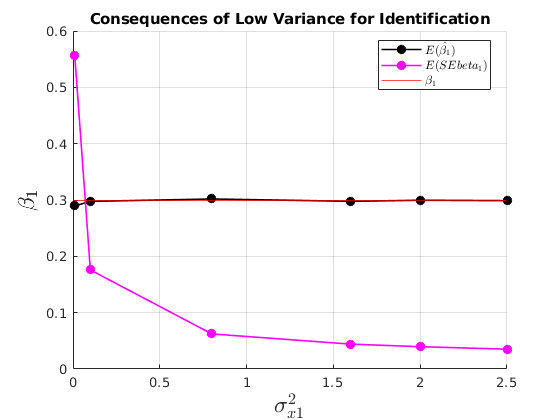
Consequences of not having enough variation for identification

figure(32)
hold on
grid on
plot(grids.sigma_x1,mu_beta(:,2),'ko-','MarkerFaceColor','k','linewidth',1.2)
plot(grids.sigma_x1,mu_SEbeta(:,2),'mo-','MarkerFaceColor','m','linewidth',1.2)
yline(par.beta1,'r')
ylabel('$\beta_{1}$','interpreter','latex','fontsize',17)
xlabel('$\sigma^{2}_{x1}$','interpreter','latex','fontsize',17)
legend({'$E(\hat{\beta_{1}})$','$E(SEbeta_{1})$','$\beta_{1}$'},'interpreter','latex','location','best')
title('Consequences of Low Variance for Identification')

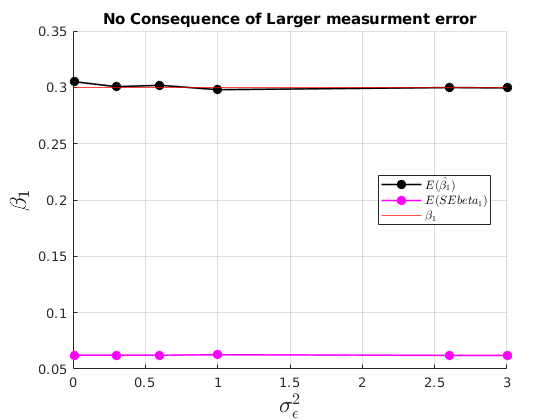
No consequences of having having a larger variance of the error

figure(31)
hold on
grid on
plot(grids.sigma_e,mu_beta(:,1),'ko-','MarkerFaceColor','k','linewidth',1.2)
plot(grids.sigma_e,mu_SEbeta(:,1),'mo-','MarkerFaceColor','m','linewidth',1.2)
yline(par.beta1,'r')
ylabel('$\beta_{1}$','interpreter','latex','fontsize',17)
xlabel('$\sigma^{2}_{\epsilon}$','interpreter','latex','fontsize',17)
legend({'$E(\hat{\beta_{1}})$','$E(SEbeta_{1})$','$\beta_{1}$'},'interpreter','latex','location','best')
title('No Consequence of Larger measurment error')

%-------------------------------------------------------------------------
% OLS
function [vars] = ols_esti(y,X)
%{
This function computes the Least Squares Estimate
Input:
y: Dependent Variable    (N,1)
X: Independent Variables (N,K)
Output:
Many stuff you saw in class.

%}
[par.Nx,par.K] 	= size(X);   % N=no.obs; K=no.regressors
[par.Ny] 	= size(y,1); %

if par.Ny~=par.Nx
    error('X and y do not have same length')
end
I = rank(X'*X) == par.K;
if I ==0
    error('Not complete Rank, Perfect Colinearity')
end
par.N = par.Nx; % Save number of regressots

vars.beta_hat  = X\y;
% Coefficients:
vars.beta_hat_alt  = inv(X'*X)*(X'*y);
% Predicted values:
vars.y_hat 	= X*vars.beta_hat;
% Residuals:
vars.e_hat 	= y-X*vars.beta_hat;
% Total Variation of the dependent variable
vars.SST 	= (y - mean(y))'*(y - mean(y));
% (SSE) Sum Squared Residuals
vars.SSE	= vars.e_hat'*vars.e_hat;
% SSR/SST or "r-squared" is the ratio of the variation in y explained by the model and the total variation of y
vars.R2 	= 1 - (vars.SSE/vars.SST);
% Adjusted "r-squared".
vars.R2A 	= 1 - (vars.SSE/(par.N-par.K))/(vars.SST/(par.N-1));

vars.sigma2_hat = vars.SSE/(par.N-par.K);

%Variance of estimator:
vars.var_covar  = vars.sigma2_hat*inv(X'*X);
vars.SEbeta_hat = sqrt(diag(vars.var_covar));

end


Published with MATLAB® R2020b