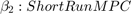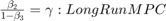Econometrics I
TA Christian Alemán
Session 5: Friday 18, February 2022
Activity 1: Simulating Consistency of OLS
Consider the model
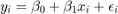
![$x\sim U[a,b]$](s5_eq07474211892256132982.png)
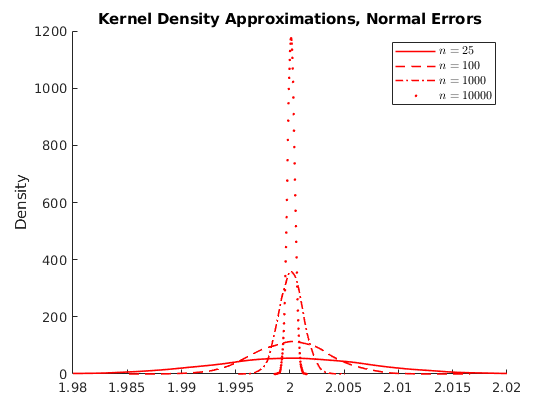
We will show consistency of 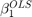
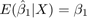
Lets assume different distributions of 
- Normal :
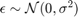
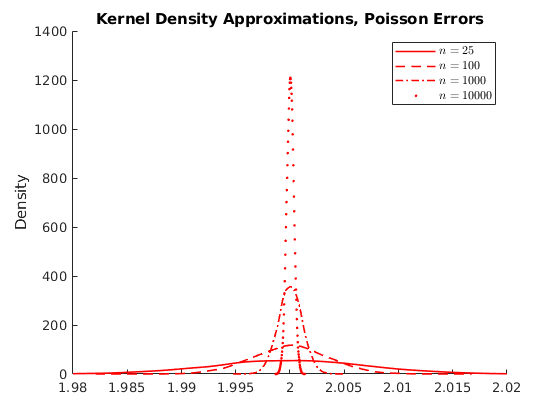
- Poisson:
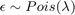
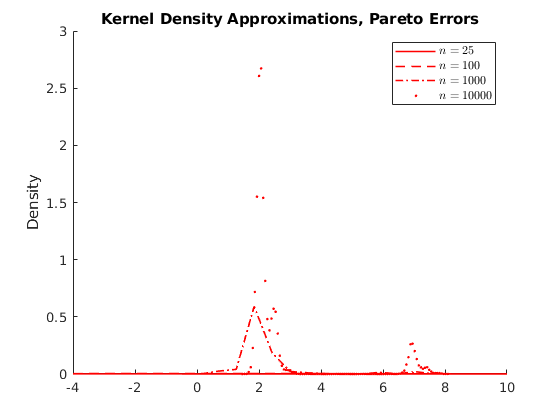
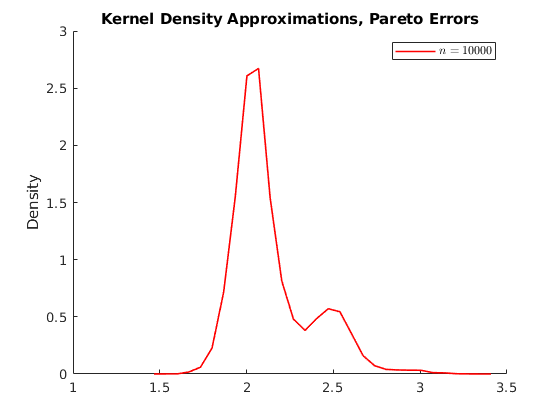
- Pareto:
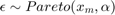
We will Simulate a population of 50000
Make 10000 draws of sample of n = [25,100,1000,10000];
% Housekeeping clc close all clear all % Set seed for reproductibility % Options opt.load_betas = 1; % 1:load betas to save time % Parameters par.N = 100000; % Population par.n_ms = 10000; % Number of MC simulations par.n_grid = [25,100,1000,10000]; % Sample size par.beta0 = 1; par.beta1 = 2; % Parameters distributions of \epsilon: par.sigma = 1; % Standard deviation normal par.lambda = 1; % Poisson Rate par.k = 1; % Shape if >=1 var is infinity try 4 par.sigma_gp = 2; % Scale par.theta = 0; par.ub = 100; par.lb = 0; % Generate population vars.e_pop = NaN(par.N,3); for i = 1:3 if i == 1 rng(123+i) vars.e_pop(:,1) = par.sigma.*randn(par.N,1); vars.e_pop(:,1) = vars.e_pop(:,1)-mean(vars.e_pop(:,1)); % demean elseif i == 2 rng(123+i) vars.e_pop(:,2) = sim_poisson(par.N,par.lambda); vars.e_pop(:,2) = vars.e_pop(:,2)-mean(vars.e_pop(:,2)); elseif i == 3 rng(123+i) vars.e_pop(:,3) = gprnd(par.k,par.sigma_gp,par.theta,par.N,1); %vars.e_pop(:,3) = sim_gp(par.N,par.k,par.sigma_gp,par.theta); vars.e_pop(:,3) = vars.e_pop(:,3)-mean(vars.e_pop(:,3)); end end vars.x_pop = unifrnd(par.lb,par.ub,par.N,1); vars.y_pop = par.beta0 +par.beta1.*repmat(vars.x_pop,1,3) +vars.e_pop; % Here we do the sampling and compute the distributions of parameters % Initialize holder vars.hbeta1 = NaN(par.n_ms,4,3); if opt.load_betas ==1 load('data') vars.hbeta1 = mc_data; else % Generate NS number of samples from the universe. for i = 1:3 % Distributions for ii = 1:4 % Sample sizes disp([i,ii]) for j = 1:par.n_ms % Number of MC simulations I_sample = randsample(par.N,par.n_grid(ii)); x_sample = vars.x_pop(I_sample); y_sample = vars.y_pop(I_sample,i); % Run regression X = [ones(par.n_grid(ii),1),x_sample]; Y = y_sample; hat_betas = X\Y; % Save betas vars.hbeta1(j,ii,i) = hat_betas(2); end end end mc_data = vars.hbeta1; save('data','mc_data') %save('data_inc','data_income') end vars.kdensity = NaN(100,4,3); % Initialize Kernel Density par.support = NaN(100,4,3); for i = 1:3 % Distributions for ii = 1:4 % Sample sizes % Do kernel approximations to smooth histograms [vars.kdensity(:,ii,i),par.support(:,ii,i)] = ksdensity(vars.hbeta1(:,ii,i),'Kernel','normal'); end end figure(1) hold on p1 = plot(par.support(:,1,1),vars.kdensity(:,1,1),'r-','linewidth',1.2); p2 = plot(par.support(:,2,1),vars.kdensity(:,2,1),'r--','linewidth',1.2); p3 = plot(par.support(:,3,1),vars.kdensity(:,3,1),'r-.','linewidth',1.2); p4 = plot(par.support(:,4,1),vars.kdensity(:,4,1),'r.','linewidth',1.2); xlim([1.98,2.02]) legend([p1 p2 p3 p4],{'$n=25$','$n=100$','$n=1000$','$n=10000$'},'interpreter','latex') title('Kernel Density Approximations, Normal Errors') ylabel('Density') figure(2) hold on p1 = plot(par.support(:,1,2),vars.kdensity(:,1,2),'r-','linewidth',1.2); p2 = plot(par.support(:,2,2),vars.kdensity(:,2,2),'r--','linewidth',1.2); p3 = plot(par.support(:,3,2),vars.kdensity(:,3,2),'r-.','linewidth',1.2); p4 = plot(par.support(:,4,2),vars.kdensity(:,4,2),'r.','linewidth',1.2); xlim([1.98,2.02]) legend([p1 p2 p3 p4],{'$n=25$','$n=100$','$n=1000$','$n=10000$'},'interpreter','latex') title('Kernel Density Approximations, Poisson Errors') ylabel('Density') figure(3) hold on p1 = plot(par.support(:,1,3),vars.kdensity(:,1,3),'r-','linewidth',1.2); p2 = plot(par.support(:,2,3),vars.kdensity(:,2,3),'r--','linewidth',1.2); p3 = plot(par.support(:,3,3),vars.kdensity(:,3,3),'r-.','linewidth',1.2); p4 = plot(par.support(:,4,3),vars.kdensity(:,4,3),'r.','linewidth',1.2); xlim([-4,10]) legend([p1 p2 p3 p4],{'$n=25$','$n=100$','$n=1000$','$n=10000$'},'interpreter','latex') title('Kernel Density Approximations, Pareto Errors') ylabel('Density') figure(4) hold on p4 = plot(par.support(1:30,4,3),vars.kdensity(1:30,4,3),'r-','linewidth',1.2); legend([p4],{'$n=10000$'},'interpreter','latex') title('Kernel Density Approximations, Pareto Errors') ylabel('Density')
Activity 1.1: Asymtotic Normality
Normality test for the last case H0: x comes from a standard normal distribution
name = {'Normal:','Poisson:','Pareto:'};
for i = 1:3
disp(name{i})
test_cdf = makedist('normal','mu',mean(vars.hbeta1(:,4,i)),'sigma',std(vars.hbeta1(:,4,i)));
%test_cdf = [vars.hbeta1(:,4,i),cdf('normal',vars.hbeta1(:,4,i),mean(vars.hbeta1(:,4,i)),std(vars.hbeta1(:,4,i)))];
h = kstest(vars.hbeta1(:,4,i),'CDF',test_cdf); % Test if the data are from the hypothesized distribution.
if h==1
disp('We reject the Null: Then distribution is not normal')
else
disp('We CANNOT reject the Null: Then distribution is normal')
end
end
Normal: We CANNOT reject the Null: Then distribution is normal Poisson: We CANNOT reject the Null: Then distribution is normal Pareto: We reject the Null: Then distribution is not normal
Activity 2: Testing Non Linear Constrains WALD test
Consider the following consumption function with different short- and long-run marginal propensities to consume (MPC).
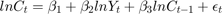
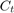 is Consumption at
is Consumption at  (in real USD)
(in real USD)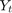 is Disposable Income at
is Disposable Income at  (in real USD)
(in real USD)
We are interested in knowing whether 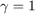
load('data_inc2') %{ 1: C0 2: C1 3: Y %} data_income = log(data_income); n = size(data_income,1); K = 3; X = [ones(n,1),data_income(:,3),data_income(:,2)]; y = data_income(:,1); % Compute OLS betas = X\y; hgamma = betas(2)/(1-betas(3)); Param = {'beta 1';'beta 2';'beta 3';'gamma'}; hat_betas = [betas;hgamma]; tab_B = table(Param,hat_betas); disp('OLS Estimates:') disp(tab_B)
OLS Estimates:
Param hat_betas
__________ _________
{'beta 1'} 0.0031416
{'beta 2'} 0.074958
{'beta 3'} 0.92462
{'gamma' } 0.99446
Predict errors
he = y-X*betas; hsigma = (he'*he)/(n-K); % Compute Asymtotic VarCovar Avar_beta = hsigma.*(inv(X'*X)); AVCV = sqrt((diag(Avar_beta))); % Variance Covariance % Compute the analytical derivatives: % Derivative: \partial beta2/(1-beta3)\partial(\beta) grad = [0;1/(1-betas(3));betas(2)/(1-betas(3))^(2)]; % Compute the asymtotic Variance Avar_Cbeta = grad'*Avar_beta*grad; % Since we are testing one restriction we compute the z-score: % H0: gamma = 1 z = (hgamma-1)./sqrt(Avar_Cbeta); disp(['Z-Score = ',num2str(z)]) disp('We cannot reject \gamma=1')
Z-Score = -0.33863 We cannot reject \gamma=1
Activity 3: Bootstrap standard errors
3.1 Non-Parametric Bootstrap
- Generate B samples with replacement of pairs
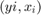
- Estimate the bootstrap
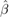 by fitting the model
by fitting the model - Compute the standard errors
par.n = par.n_grid(3); % Sample size par.K = 2; vars.x =1+2*randn(par.n,2) ; vars.x(:,1) =4+vars.x(:,1); vars.e =2*randn(par.n,1) ; vars.y = vars.x*ones(2 ,1) + vars.e ; if par.K ==3 vars.x = [ones(par.n,1),vars.x]; vars.y = par.beta0+vars.x(:,2:end)*ones(2 ,1) + vars.e ; end vars.hbeta = vars.x\vars.y ; vars.ehat = vars.y-vars.x*vars.hbeta; par.B = 1000;% hbeta_sample =NaN(par.B,par.K); for i = 1:par.B I_sample = ceil(par.n*rand(1,par.n)); ysample = vars.y(I_sample); xsample(:,1) = vars.x(I_sample,1); xsample(:,2) = vars.x(I_sample,2); hbeta_sample(i,:) = (xsample\ysample)'; end diff = hbeta_sample-repmat(vars.hbeta',par.B,1); bootVCV = diff'*diff/par.B; OLSVCV = (vars.e'*vars.e)/par.n*inv(vars.x'*vars.x); vars.SEbeta_hat_OLS = sqrt(diag(OLSVCV)); vars.SEbeta_hat_boot = sqrt(diag(bootVCV)); Param = {'beta 0';'beta 1'}; if par.K ==3 Param = {'beta 0';'beta 1','beta2'}; end SE_OLS = vars.SEbeta_hat_OLS; SE_Bootstrap = vars.SEbeta_hat_boot; tab_SE = table(Param,SE_OLS,SE_Bootstrap); disp('Non-Parametric Standard Errors:') disp(tab_SE)
Non-Parametric Standard Errors:
Param SE_OLS SE_Bootstrap
__________ ________ ____________
{'beta 0'} 0.012984 0.012932
{'beta 1'} 0.031073 0.030937
3.2 Parametric Bootstrap
- Generate 2*B samples with replacement of
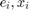 indepedently
indepedently - Construct values of
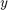
- Estimate the bootstrap
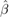 by fitting the model
by fitting the model - Compute the standard errors
for i = 1:par.B I_sample = ceil(par.n*rand(1,par.n)); II_sample = ceil(par.n*rand(1,par.n)); esample = vars.ehat(I_sample); xsample(:,1) = vars.x(I_sample,1); xsample(:,2) = vars.x(I_sample,2); ysample = xsample*vars.hbeta+esample; hbeta_sample(i,:) = (xsample\ysample)'; end diff = hbeta_sample-repmat(vars.hbeta',par.B,1); bootVCV = diff'*diff/par.B; OLSVCV = (vars.e'*vars.e)/par.n*inv(vars.x'*vars.x); vars.SEbeta_hat_OLS = sqrt(diag(OLSVCV)); vars.SEbeta_hat_boot = sqrt(diag(bootVCV)); SE_OLS = vars.SEbeta_hat_OLS; SE_Bootstrap = vars.SEbeta_hat_boot; tab_SE = table(Param,SE_OLS,SE_Bootstrap); disp('Parametric Standard Errors:') disp(tab_SE) dert_stop = 1; %----------------------------------------------------------- function data = sim_gp(N,k,sigma,theta) % This function simulates a vector data for the generalized Pareto using the inverse % CDF method: %{ Inputs: N : Number of observations to be simulated k : Index Shape \chi sigma : Scale theta : Threshold location \mu Output: data : NX1 vector of data With shape ξ > 0 and location μ = σ / ξ the GPD is equivalent to the Pareto distribution with scale x m = σ / ξ and shape α = 1 / ξ %} var_x = rand(N,1); data = sigma./k.*((1-var_x).^(-k)-1)+theta; end %----------------------------------------------------------- function data = sim_poisson(N,lambda) % This function simulates a vector data for the generalized Poisson Distribution using the inverse % CDF method: %{ Inputs: N : Number of observations to be simulated lambda : Poisson rate Output: data : NX1 vector of data %} var_x = rand(N,1); data = icdf('Poisson',var_x,lambda); end
Parametric Standard Errors:
Param SE_OLS SE_Bootstrap
__________ ________ ____________
{'beta 0'} 0.012984 0.01324
{'beta 1'} 0.031073 0.030953