Econometrics I

TA Christian Alemán

Session 6: Friday 25, February 2022

Activity 1: Hetoskedasticity

Simulating Hetoskedasticity

1.1: With Normal Errors:

Consider the model

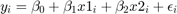
$y_{i} = \beta_{0}+\beta_{1}x1_{i}+\beta_{2}x2_{i}+\epsilon_{i}$

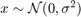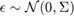
$x\sim \mathcal{N}(0,\sigma^{2})$ and $\epsilon \sim \mathcal{N}(0,\Sigma)$

$\Sigma=\left[\begin{array}{cccc} \sigma^{2}_{1}&0& \dots &0 \\ 0&\sigma^{2}_{2}&\dots&\vdots \\ \vdots&\vdots&\ddots&\vdots \\ 0&\dots&0&\sigma^{2}_{n} \end{array}\right]$

% Housekeeping
clear all
close all
clc
% Set the seed
rng(123)

% Parameters

par.beta0 = 1;      % Intercept
par.beta1 = 2;      % Slope
par.n = 200;

% Simulate the Data Generating process

k = 3;
vars.x = randn(par.n,k-1);
vars.eho = (2) .* randn(par.n,1); % heteroscedastic errors
vars.ehe = (1+vars.x(:,k-1)) .* randn(par.n,1); % heteroscedastic errors
vars.y = par.beta0 + par.beta1.*vars.x(:,1)+ par.beta1.*vars.x(:,2)  + vars.ehe;

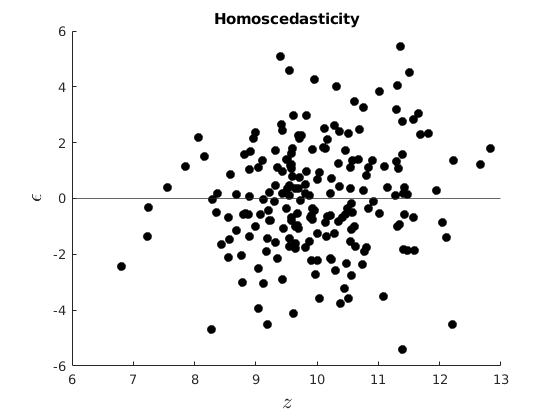
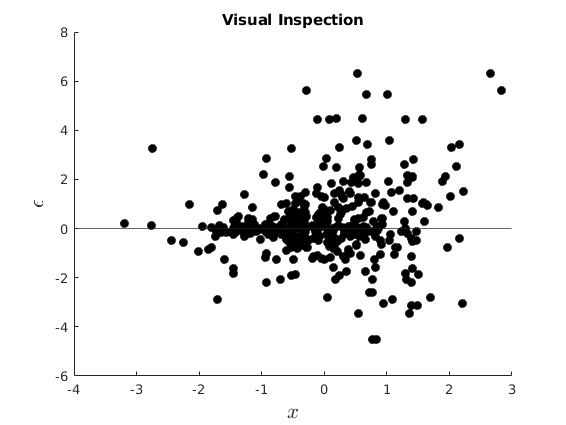
Plot our conditional residuals

figure(1)
hold on
plot(10+vars.x(:,k-1),vars.eho,'ko','MarkerFaceColor','k')
yline(0)
xlabel('$z$','interpreter','latex','Fontsize',16)
ylabel('$\epsilon$','interpreter','latex','FontSize',16)
title('Homoscedasticity')
figure(2)
hold on
plot(10+vars.x(:,k-1),vars.ehe,'ko','MarkerFaceColor','k')
yline(0)
xlabel('$z$','interpreter','latex','Fontsize',16)
ylabel('$\epsilon$','interpreter','latex','Fontsize',16)
title('Heteroscedasticity')

% Estimate OLS
[beta,sigma,e,se,se_rob] = my_ols(vars.y,[ones(par.n,1),vars.x]);
t=table(beta,se,se_rob);
disp(t)

     beta       se       se_rob 
    ______    _______    _______

    1.2525    0.10352    0.10418
    2.2279    0.11922    0.11104
    2.2043    0.10046    0.14658

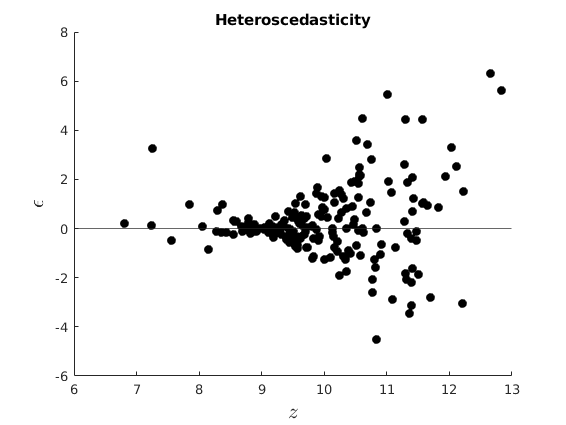
Visual Inspection

figure(3)
hold on
plot(vars.x,vars.ehe,'ko','MarkerFaceColor','k')
yline(0)
xlabel('$x$','interpreter','latex','Fontsize',16)
ylabel('$\epsilon$','interpreter','latex','Fontsize',16)
title('Visual Inspection')

White Test

$H_{0}:$ Homoscedasticity

[value, pvalue] = my_white(e,[ones(par.n,1),vars.x]);
t = table(pvalue);
disp(t)
if pvalue<0.05
    disp('Reject Homoscedasticity')
else
    disp('Cannot Reject Homoscedasticity')
end

      pvalue  
    __________

    9.3292e-10

Reject Homoscedasticity

Estimate GLS

opt.het = 1;        % Heteroskedasticity
[beta_gls,e,se_gls] = my_gls(vars.y,[ones(par.n,1),vars.x],opt);

betas_1 =  [beta(2);NaN;beta_gls(2)];
method = {'OLS';'E-White';'FGLS'};
s_err = [se(2);se_rob(2);se_gls(2)];
t = table(method,betas_1,s_err);
disp(t)

Lets Compute Bootstrap SE

par.B = 1000;%
par.K = k;
hbeta_sample =NaN(par.B,par.K);

for i = 1:par.B
    rng(i)
    I_sample = ceil(par.n*rand(par.n,1));
    ysample = vars.y(I_sample);
    xsample = vars.x(I_sample,:);

    hbeta_sample(i,:)  = ([ones(par.n,1),xsample]\ysample)';
end
diff = hbeta_sample-repmat(beta',par.B,1);
bootVCV = diff'*diff/par.B;
vars.SEbeta_hat_boot = sqrt(diag(bootVCV));

disp('Results Using Our Functions')
betas_1 =  [beta(2);NaN;beta_gls(2);mean(hbeta_sample(:,2))];
method = {'OLS';'E-White';'FGLS';'Bootstrap'};
s_err = [se(2);se_rob(2);se_gls(2);vars.SEbeta_hat_boot(2)];
t = table(method,betas_1,s_err);
disp(t)

% Lets compare with the matlab inbuilt functions:
[~,mse_rob,~] = hac(vars.x,vars.y,'type','HC','display','off');
[coeff,se_gls] = fgls(vars.x,vars.y,'innovMdl','HC0','display','off');
m1 = fitlm(vars.x,vars.y);
se_ols = m1.Coefficients.SE;
coeff_ols = m1.Coefficients.Estimate;

disp('Results Using Inbuilt Matlab')
betas_1 =  [coeff_ols(2);NaN;coeff(2)];
method = {'OLS';'E-White';'FGLS'};
s_err = [se_ols(2);mse_rob(2);se_gls(2)];
t = table(method,betas_1,s_err);
disp(t)

Results Using Our Functions
       method        betas_1      s_err  
    _____________    _______    _________

    {'OLS'      }    2.2279       0.11922
    {'E-White'  }       NaN       0.11104
    {'FGLS'     }    2.2286     0.0060634
    {'Bootstrap'}    2.2264       0.11177

Results Using Inbuilt Matlab
      method       betas_1      s_err  
    ___________    _______    _________

    {'OLS'    }    2.2279       0.12013
    {'E-White'}       NaN       0.11104
    {'FGLS'   }    2.2286     0.0061093

1.2: With Uniform Errors:

Consider the model

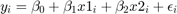
$y_{i} = \beta_{0}+\beta_{1}x1_{i}+\beta_{2}x2_{i}+\epsilon_{i}$

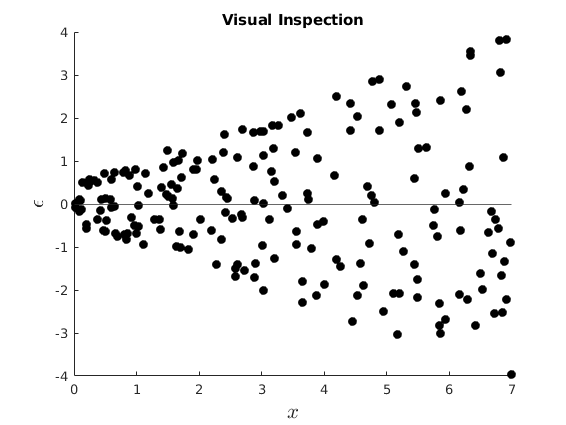
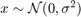$x\sim \mathcal{N}(0,\sigma^{2})$ and $\epsilon \sim U[-z,z]$

Estimate OLS

par.ub = 100;
par.lb = 0;
aux_z = rand(par.n,1).*7;

vars.ehe = ((20+10*aux_z)).*(rand(par.n,1)-0.5);
vars.x(:,1) = unifrnd(par.lb,par.ub,par.n,1);
vars.x(:,2) = aux_z;
vars.y = par.beta0 +par.beta1.*vars.x(:,1) +par.beta1.*vars.x(:,2) +vars.ehe;


k = 3;
%vars.x = randn(par.n,k-1);
vars.ehe = (1+vars.x(:,k-1)) .*(rand(par.n,1)-0.5); % heteroscedastic errors
vars.y = par.beta0 + par.beta1.*vars.x(:,1)+ par.beta1.*vars.x(:,2)  + vars.ehe;

[beta,sigma,e,se,se_rob] = my_ols(vars.y,[ones(par.n,1),vars.x]);

Visual Inspection

figure(4)
hold on
plot(vars.x(:,2),vars.ehe,'ko','MarkerFaceColor','k')
yline(0)
xlabel('$x$','interpreter','latex','Fontsize',16)
ylabel('$\epsilon$','interpreter','latex','Fontsize',16)
title('Visual Inspection')

White Test

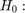$H_{0}:$ Homoscedasticity

[value, pvalue] = my_white(e,[ones(par.n,1),vars.x]);
t = table(pvalue);
disp(t)
if pvalue<0.05
    disp('Reject Homoscedasticity')
else
    disp('Cannot Reject Homoscedasticity')
end

      pvalue  
    __________

    8.8041e-14

Reject Homoscedasticity

Estimate GLS and Bootstrap SE

[beta_gls,~,se_gls] = my_gls(vars.y,[ones(par.n,1),vars.x],opt);

par.B = 1000;%
par.K = k;
hbeta_sample =NaN(par.B,par.K);

for i = 1:par.B
    rng(i)
    I_sample = ceil(par.n*rand(par.n,1));
    ysample = vars.y(I_sample);
    xsample = vars.x(I_sample,:);

    hbeta_sample(i,:)  = ([ones(par.n,1),xsample]\ysample)';
end
diff = hbeta_sample-repmat(beta',par.B,1);
bootVCV = diff'*diff/par.B;
vars.SEbeta_hat_boot = sqrt(diag(bootVCV));

disp('Results Using our own functions')
betas_1 =  [beta(2);NaN;beta_gls(2);mean(hbeta_sample(:,2))];
method = {'OLS';'E-White';'FGLS';'Bootstrap'};
s_err = [se(2);se_rob(2);se_gls(2);vars.SEbeta_hat_boot(2)];
t = table(method,betas_1,s_err);
disp(t)

% Lets compare with the matlab inbuilt functions:
[~,mse_rob,~] = hac(vars.x,vars.y,'type','HC','display','off');
[coeff,se_gls] = fgls(vars.x,vars.y,'innovMdl','HC0','display','off');
m1 = fitlm(vars.x,vars.y);
se_ols = m1.Coefficients.SE;
coeff_ols = m1.Coefficients.Estimate;

disp('Results Using Inbuilt Matlab')
betas_1 =  [coeff_ols(2);NaN;coeff(2)];
method = {'OLS';'E-White';'FGLS'};
s_err = [se_ols(2);mse_rob(2);se_gls(2)];
t = table(method,betas_1,s_err);
disp(t)

Results Using our own functions
       method        betas_1      s_err   
    _____________    _______    __________

    {'OLS'      }     1.999      0.0035595
    {'E-White'  }       NaN      0.0032256
    {'FGLS'     }    1.9992     0.00033118
    {'Bootstrap'}    1.9992      0.0033158

Results Using Inbuilt Matlab
      method       betas_1      s_err  
    ___________    _______    _________

    {'OLS'    }     1.999     0.0035865
    {'E-White'}       NaN     0.0032256
    {'FGLS'   }    1.9992     0.0003337

Activity 2: Autocorrelated Errors

Simulating AR(1) errors

Consider the model

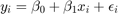
$y_{i} = \beta_{0}+\beta_{1}x_{i}+\epsilon_{i}$

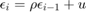
$x\sim U[a,b]$ and $\epsilon_{i} = \rho\epsilon_{i-1}+u$

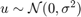
and $u \sim \mathcal{N}(0,\sigma^{2})$

$\Sigma=\left[\begin{array}{ccccc} 1&\rho& \rho^{2}& \dots &\rho^{n-1} \\ \rho&1&\dots&\dots&\rho^{n-2} \\ \rho^{2}&\vdots&1&\vdots&\vdots \\ \vdots&\vdots&\vdots&1&\rho \\ \rho^{n-1}&\dots&\dots&\dots&1 \end{array}\right]$

par.rho = 0.9;
vars.eau = NaN(par.n,1);
vars.eau(1,1) = randn(1,1)/sqrt(1-par.rho^2);  % The trend of the AR(1) process
for i = 2:par.n
    rng(12300+i)
  vars.eau(i,1) = par.rho*vars.eau(i-1,1) + 5*randn(1,1); %
end
%par.ub = 100;
%par.lb = 0;
%vars.x = unifrnd(par.lb,par.ub,par.n,1);
vars.y = par.beta0 +par.beta1.*vars.x(:,1)+par.beta1.*vars.x(:,2) +vars.eau;

[beta,sigma,e,se,~] = my_ols(vars.y,[ones(par.n,1),vars.x]);
se_rob=my_newey(e,[ones(par.n,1),vars.x],1);

Visual Inspection

figure(5)
hold on
plot(e(2:end),e(1:end-1),'ko','MarkerFaceColor','k')
yline(0)
xlabel('$\epsilon_{t-1}$','interpreter','latex','Fontsize',16)
ylabel('$\epsilon_{t}$','interpreter','latex','Fontsize',16)
title('Visual Inspection')

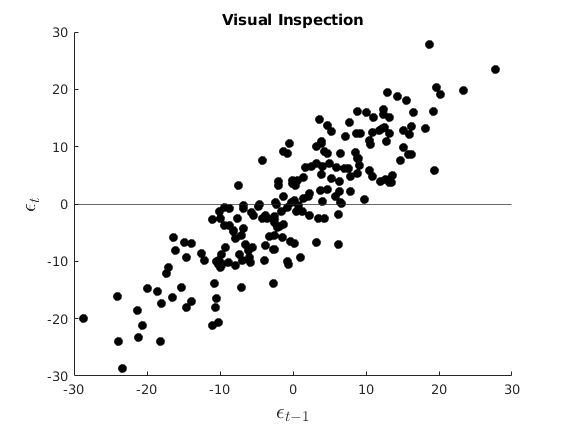
DW Durbin Watson

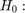$H_{0}:$ No Autocorrelation

pvalue = dwtest(e,[ones(par.n,1),vars.x]);
t = table(pvalue);
disp(t)
if pvalue<0.05
    disp('Reject Null: there is autocorrelation')
else
    disp('Cannot Reject Null; There is no autocorrelation')
end

      pvalue  
    __________

    1.3004e-64

Reject Null: there is autocorrelation

Estimate GLS and Bootstrap SE

opt.het = 0;
[beta_gls,e,se_gls] = my_gls(vars.y,[ones(par.n,1),vars.x],opt);
par.B = 1000;%
par.K = k;
hbeta_sample =NaN(par.B,par.K);

for i = 1:par.B
    rng(i)
    I_sample = ceil(par.n*rand(par.n,1));
    ysample = vars.y(I_sample);
    xsample = vars.x(I_sample,:);

    hbeta_sample(i,:)  = ([ones(par.n,1),xsample]\ysample)';
end
diff = hbeta_sample-repmat(beta',par.B,1);
bootVCV = diff'*diff/par.B;
vars.SEbeta_hat_boot = sqrt(diag(bootVCV));

disp('Using our functions')
betas_1 =  [beta(2);NaN;beta_gls(2);mean(hbeta_sample(:,2))];
method = {'OLS';'Newey West';'FGLS';'Bootstrap'};
s_err = [se(2);se_rob(2);se_gls(2);vars.SEbeta_hat_boot(2)];
t = table(method,betas_1,s_err);
disp(t)

% Lets compare with the matlab inbuilt functions:
[~,mse_rob,~] = hac(vars.x,vars.y,'type','HAC','bandwidth',floor(4*(par.n/100)^(2/9))+1,'weights','BT','display','off');
[coeff,se_gls] = fgls(vars.x,vars.y,'display','off');
m1 = fitlm(vars.x,vars.y);
se_ols = m1.Coefficients.SE;
coeff_ols = m1.Coefficients.Estimate;

disp('Results Using Inbuilt Matlab')
betas_1 =  [coeff_ols(2);NaN;coeff(2)];
method = {'OLS';'Newey West';'FGLS'};
s_err = [se_ols(2);mse_rob(2);se_gls(2)];
t = table(method,betas_1,s_err);
disp(t)

End of Code

%---------------------------------------------------------
function [beta,e,se] = my_gls(y,x,opt)
%{
This function computes GLS estimates and
its standard errors
inputs: y dependent var
        x independent vars
outputs: beta   OLS coefficients
         sigma  Estimator or variance of error
         e      Backed residuals
         se     Standard Errors
%}
    n = size(x,1);
    if opt.het==1
        % Tradicional heteroskedasticity
        [~,~,e_ols] = my_ols(y, x);
        e_ols = e_ols.^2;
        %C = diag(1./ sqrt(e_ols));
        C = chol(inv(diag(e_ols)));
        [beta,~,e,se] = my_ols(C*y, C*x);
    else
        % AR(1) Errors
        [~,~,e_ols] = my_ols(y, x);

        % estimation of AR(1) coefficient
        ey = e_ols(2:n);
        ex = e_ols(1:n-1);
        rho = ex\ey;            % Estimating the autocorrelation coeff
        e_auto = ey-ex*rho;
        var_e = var(e_auto);

        %factor = eye(n).*var_e./(1-rho^2);     % Cancels out
        sigma_e = eye(n);
        for i = 1:n
            for j = i+1:n
                sigma_e(i,j) = rho^(j-i);
                sigma_e(j,i) = sigma_e(i,j);
            end
        end
        %sigma_e = factor.*sigma_e;
        C = chol(inv(sigma_e));
        [beta,~,e,se] = my_ols(C*y, C*x);
    end % end if
end
%---------------------------------------------------------
function [beta,sigma,e,se,se_rob] = my_ols(y,x)
%{
This function computes OLS estiamtes and
its standard errors
inputs: y dependent var
        x independent vars
outputs: beta   OLS coefficients
         sigma  Estimator or variance of error
         e      Backed residuals
         se     Standard Errors
%}
    [n,k] = size(x);
    beta = x\y;
    sigma = (y-x*beta)'*(y-x*beta)/(n-rank(x));
    e = y - x*beta;
    VCV = (e'*e)/n*inv(x'*x);
    se = sqrt(diag(VCV));

    % Eicker-White se
   aux = x.*(kron(e.^2,ones(1,k)));
	VCV_white = inv(x'*x) * x'*aux* inv(x'*x);


    se_rob = sqrt(diag(VCV_white));
end
%---------------------------------------------------------
function [value, pvalue] = my_white(e, x)
%{
 White's test for heteroscedasticity
 Input:
	e: Residuals
	x: Independent Variables
%}
	n = size(e,1);
	k = size(x,2) - 1;
	[~,~,e_ols] =my_ols(e.^2,x);
    TSS = e.^2 - mean(e.^2);
	TSS = TSS' * TSS;
	ESS = e_ols' * e_ols;
	rsq = 1 - ESS / TSS;  % the r-square auxiliary
	value = n*rsq;                  % Statistic
	pvalue = 1 - chi2cdf(value,k);  % Value
end

function [se]= my_newey(e,x,lag)
%{
% Compute Newey West Standard errors
Input: e: residuals
       x: Matrix of regressors
       lag: number of langs

%}
[N,k] = size(x);
VT = 0;     % This I will fill on a loop,
for s = 0:lag
    omega_s = 1-s/(lag+1);
    for t = s+1:N
        if (s==0)
            VT = VT+e(t)^2*x(t,:)'*x(t,:);
        else        % This calculates the off-diagonal terms
            VT = VT+omega_s*e(t)*e(t-s)*(x(t,:)'*x(t-s,:)+x(t-s,:)'*x(t,:));
        end
    end
end
VT = (1/(N-k)) .*VT;
se = sqrt(diag(N.*(inv(x'*x)*VT*inv(x'*x))));
end

      method       betas_1      s_err  
    ___________    _______    _________

    {'OLS'    }    2.2279       0.11922
    {'E-White'}       NaN       0.11104
    {'FGLS'   }    2.2286     0.0060634